Forskel mellem definite og indefinite integraler Forskel Mellem
Calculus er en vigtig gren af matematik, og differentiering spiller en afgørende rolle i calculus. Den omvendte proces af differentieringen er kendt som integration, og den inverse er kendt som integralet, eller simpelthen sætter den invers af differentiering en integrering. Baseret på de resultater, de producerer integralerne er opdelt i to klasser, f.eks., bestemte og ubestemte integraler.
Definitivt integreret
- 9 ->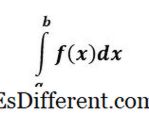
Det bestemte integral af f (x) er et NUMBER og repræsenterer området under kurven f (x) fra x = a til x = b .
Et bestemt integral har øvre og nedre grænser på integralerne, og det kaldes bestemt fordi, i slutningen af problemet har vi et tal - det er et klart svar.
Ubestemt Integral

Den ubestemte integral af f (x) er en FUNCTION og svarer på spørgsmålet "Hvilken funktion, når differentieret giver f (x) ? "
Med en ubestemt integreret er der ingen øvre og nedre grænser for integralet her, og hvad vi får er et svar, der stadig har x 's i det og vil også have en konstant (sædvanligvis betegnet C ) i den.
Ubestemt integreret giver normalt en generel løsning på differentialekvationen.
Ubestemt integral er mere af en generel integrationsform, og den kan fortolkes som anti-derivatet af den betragtede funktion.
Antag, at differentiering af funktionen F fører til en anden funktion f , og integrationen af f giver integralet. Symbolisk er dette skrevet som
F (x) = ∫ƒ (x) dx
eller
F = ∫ƒ dx
hvor både F og ƒ < er funktioner af x , og F er differentierbar. I ovennævnte form kaldes det en Reimann integral, og den resulterende funktion ledsager en vilkårlig konstant. En ubestemt integral producerer ofte en familie af funktioner; derfor er integralet ubestemt.
Integraller og integrationsprocesser er kernen i løsningen af differentialligninger. I modsætning til trinene i differentiering følger trinene i integration imidlertid ikke altid en klar og standard rutine. Af og til ser vi, at løsningen ikke udtrykkeligt kan udtrykkes i form af elementær funktion. I så fald gives den analytiske løsning ofte i form af et ubestemt integreret.
Grundlæggende sætning af beregning
Det definitive og det ubestemte integral er forbundet med grundlægningen af beregningen som følger: For at beregne en
bestemt integral , find ubestemt integreret > (også kendt som anti-derivatet) af funktionen og evaluere ved endepunkterne x = a og x = b . Forskellen mellem bestemte og ubestemte integraler vil være tydelig, når vi vurderer integralerne for den samme funktion. Overvej følgende integral:
OK. Lad os gøre begge dem og se forskellen.
For integration skal vi tilføje et til indekset, der fører os til følgende udtryk:

På dette tidspunkt er
C
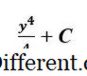
kun en konstant for os. Yderligere oplysninger er nødvendige i problemet for at bestemme den nøjagtige værdi af C . Lad os evaluere det samme integral i sin bestemte form i. e., med de øvre og nedre grænser inkluderet. Vi beregner nu grafisk område under kurven
f (x) = y

3 mellem y = 2 og y = 3 >. Det første trin i denne evaluering er det samme som den ubestemte integrerede evaluering. Den eneste forskel er, at denne gang omkring tilføjer vi ikke konstant C .
Udtrykket i dette tilfælde ser ud som følger: Dette drejer fører til: I det væsentlige erstattede vi 3 og derefter 2 i udtrykket og opnåede forskellen mellem dem.
Dette er den bestemte værdi i modsætning til brugen af konstant

C

tidligere.
Lad os undersøge den konstante faktor (med hensyn til ubestemt integreret) i mere detaljeret omfang. Hvis differencen på y
3
er 3y 2 , så ∫ 3y 2
dy = y 3 Men 3y 2
kunne være forskellen mellem mange udtryk, hvoraf nogle omfatter y 3 -5 , > y 3 +7 , osv. … Dette indebærer, at vendingen ikke er unik, da konstanten ikke er klarlagt under operationen. Så generelt er 3y 2 forskellen mellem
y 3 + C hvor C er en hvilken som helst konstant. I øvrigt er C kendt som 'konstant for integration' . Vi skriver dette som: ∫ 3y 2
. dx = y
3 + C Integrationsteknikker til ubestemt integrering, f.eks. Tabellen opslag eller Risch integration, kan tilføje nye diskontinuiteter under integrationsprocessen. Disse nye diskontinuiteter forekommer, fordi anti-derivaterne kan kræve indførelse af komplekse logaritmer. Komplekse logaritmer har en springdiskontinuitet, når argumentet krydser den negative reelle akse, og integrationsalgoritmerne kan undertiden ikke finde en repræsentation, hvor disse hopper annullerer.



