Forskel mellem integration og summation: integration vs summation sammenlignet
Integration vs Summation
I ovenstående gymnasiale matematik findes integration og opsummering ofte i matematiske operationer. De er tilsyneladende brugt som forskellige værktøjer og i forskellige situationer, men de deler et meget tæt forhold.
Mere om Summation
Summation er driften af at tilføje en sekvens af tal, og operationen er ofte betegnet af det græske brev af kapital sigma Σ. Det bruges til at forkorte summen og svare til summen / summen af sekvensen. De bruges ofte til at repræsentere serien, som i det væsentlige er uendelige sekvenser opsummeret. De kan også bruges til at angive summen af vektorer, matricer eller polynomier.
Summen foretages normalt for en række værdier, der kan repræsenteres af et generelt udtryk, såsom en serie, der har en fælles betegnelse. Udgangspunktet og slutpunktet for summationen er kendt som henholdsvis den nedre og den øvre grænse for summationen.
F.eks. Summen af sekvensen a 1 , a 2 , a 3 , a 4 , …, en n er en 1 + a 2 + a 3 + … + a n som let kan repræsenteres ved hjælp af summationsnotationen som Σ n i = 1 a i ; jeg hedder summationsindekset.
Mange variationer bruges til summen baseret på ansøgningen. I nogle tilfælde kan den øvre grænse og nedre grænse angives som et interval eller et interval, såsom Σ 1≤i≤100 a i og Σ i∈ [1, 100] a i . Eller det kan gives som et sæt tal som Σ i∈P a i , hvor P er et defineret sæt.
I nogle tilfælde kan to eller flere sigma tegn anvendes, men de kan generaliseres som følger; Σ j Σ k a jk = Σ j, k a jk .
Også summeringen følger mange algebraiske regler. Da den indlejrede operation er tilføjelsen, kan mange af de almindelige regler for algebra anvendes på summen selv og for de individuelle udtryk, der er afbildet i opsummeringen.
Mere om integration
Integrationen defineres som den omvendte proces af differentiering. Men i sin geometriske visning kan det også betragtes som det område, der er omsluttet af funktionens og aksens kurve. Derfor giver beregningen af området værdien af et bestemt integral som vist i diagrammet.
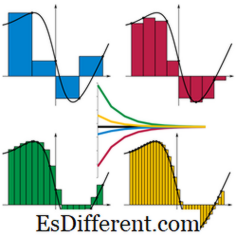
Billedkilde: // da. wikipedia. org / wiki / fil: Riemann_sum_convergence. png
Værdien af det bestemte integral er faktisk summen af de små strimler inde i kurven og aksen.Området for hver strimmel er højden × bredden ved punktet på den betragtede akse. Bredde er en værdi, vi kan vælge, siger Δx. Og højden er omtrent værdien af funktionen på det betragtede punkt, siger f (x i ). Fra diagrammet er det tydeligt, at jo mindre strimlerne er bedre, strimlerne passer ind i det afgrænsede område, og dermed bedre tilnærmelse af værdien.
Så generelt er det bestemte integral I mellem punkterne a og b (i. E i intervallet [a, b] hvor a
f
(x i ) Δx f (x) dx Dette er kendt som Reimann Integral of the funktion f (x) i intervallet [a, b]. I dette tilfælde er a og b kendt som integralens øvre grænse og nedre grænse. Reimann integral er en grundlæggende form for alle integrationsmetoder. I det væsentlige er integration summen af området, når rektangelets bredde er uendelig. Hvad er forskellen mellem integration og opsummering? • Summation er tilføjelse af en sekvens af tal. Normalt er summen angivet i denne formular Σ n i = 1 a i, når ordene i sekvensen har et mønster og kan udtrykkes ved hjælp af en generel term.
• Integration er stort set det område, der er afgrænset af funktionens kurve, akse og øvre og nedre grænse. Dette område kan gives som summen af meget mindre områder inkluderet i det afgrænsede område. • Summation involverer de diskrete værdier med de øvre og nedre grænser, mens integrationen involverer kontinuerlige værdier. • Integration kan fortolkes som en speciel form for opsummering.
• I numeriske beregningsmetoder udføres integration altid som en summering.