Forskel mellem divisor og dividende

Divisor vs Dividend

Tilføjelse, subtraktion, multiplikation og division er de fire grundlæggende aritmetiske operationer udført i sæt af reelle tal. Division er den inverse funktion af multiplikation. For eksempel

og derfor

. I modsætning til de andre tre operationer er division ikke lukket i sæt af heltal. For eksempel er

ikke et helt tal. Med andre ord er der undertiden en rest tilbage, når et nummer er opdelt af en anden. For at gøre divisionens drift færdig, udvides nummersystemet fra sæt af heltal til sæt af rationelle tal.

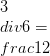
I sæt af heltal spiller divisionalgoritmen en stor rolle, hvad division angår. Det står, at der for hvert heltal a, b (≠ 0) findes unike heltal q og r sådan at a = bq + r, hvor 0 ≤ q ≤ | b |. Hvis du f.eks. Tager a = 5 og b = 2, er de unikke værdier for q og r henholdsvis 2 og 1, som 5 = 2 * 2 + 1. Dette viser at når 5 er divideret med 2 i sæt af heltal, er svaret 2 og en rest af 1 tilbage.

Men i sæt af reelle tal er divisionen ingen rest. Lad

a, b (≠ 0) være to reelle tal, så hvis og kun hvis

Hvad er en divisor?

Overvej tallet

b dividerer tallet a, i. e.. Tallet

a er divideret med tallet b. Siden nummeret b er nummeret, som et andet nummer er opdelt på, kaldes det divisoren - divisionens dommer. For eksempel overveje sagen om at dividere 5 med 2. Derefter er divisoren 2. En meget vigtig ting at notere om divisoren er, at den er ikke-nul. Det skyldes, at division med 0 ikke er defineret.

Hvad er et udbytte?

Overvej eksemplet i det foregående eksempel. Der er

a det tal, der er divideret med b - divisoren. Tallet a, som skal deles, hedder udbyttet. I eksemplet på 5 er divideret med 2, er 5 udbyttet. Således er divisionsalgoritmen

a udbyttet, og b er divisoren. Hvad er forskellen mellem divisor og udbytte?

• Udbytte er det tal, der er opdelt. Det nummer, hvorfra udbyttet er opdelt, hedder divisoren. • Udbytte kan være en reel værdi, mens divisor skal være ikke-nul. Anbefalede Forskel mellem emission og absorptionsspektra Forskel mellem emic og etic | Emic vs Etic Forskel mellem emission og stråling