Forskel mellem Power Series og Taylor Series

Power Series vs Taylor Series

I matematik er en reel sekvens en ordnet liste over reelle tal. Formelt er det en funktion fra sæt af naturlige tal ind i sæt af reelle tal. Hvis a _n er n ^{termen af ​​en sekvens, betegner vi sekvensen ved eller ved} a 1 , a 2 _{, …, a} n, _{…. Se f.eks. Sekvensen 1, ½, ⅓, …,} 1 ^/ n _{, …. Det kan betegnes som {1 / n}.}

Det er muligt at definere en serie ved hjælp af sekvenser. En serie er summen af ​​vilkårene i en sekvens. Derfor er der for hver sekvens en associeret sekvens og vice versa. Hvis {a n} _{er den pågældende sekvens, kan serien dannet af den sekvens repræsenteres som:} I det ovenstående eksempel er den tilknyttede serie således 1+

1

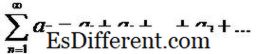
/ ² + ₁ / ³ + … + ₁ / ⁿ + …. _{Som navne antyder, er strømserien en særlig type serie, og den anvendes i vid udstrækning i Numerisk Analyse og relateret matematisk modellering. Taylor-serien er en speciel power-serie, der giver en alternativ og nem at manipulere måde at repræsentere kendte funktioner på.}

Hvad er Power-serien?

En power-serie er en serie af formularen

som er konvergent (muligvis) for noget interval centreret ved

c

. Koefficienterne a n kan være reelle eller komplekse tal og er uafhængige af _{x; jeg. e.} Dummy-variablen. For eksempel ved at indstille a

n = 1 for hver _n, og c = 0, strømserien 1 + x + x 2 + … + x ⁿ + … opnås. Det er let at bemærke, at når x ε (-1, 1) konvergerer denne strømserie til 1 / (1-x).

En strømserie konvergerer når

x

= c. De andre værdier på x, som strømserien konvergerer, vil altid have form af et åbent interval centreret ved c. Det er, der vil være en værdi 0 < R ≤ ∞ sådan at for hver x tilfredsstillende | xc | ≤ R er strømserien konvergent, og for hver x tilfredsstillende | xc |> R er strømserien afvigende. Denne værdi R kaldes konvergensradius af kraftserien (R kan tage nogen reel værdi eller positiv uendelighed).

Power-serier kan tilføjes, subtraheres, multipliceres og deles ved hjælp af følgende regler. Overvej de to strømserier:. Så

i. e.

Som udtryk tilføjes eller subtraheres sammen. Det er også muligt at multiplicere og opdele de to strømserier ved hjælp af identiteten, Hvad er Taylor-serien?

Taylor-serien er defineret for en funktion

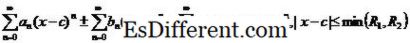
f (

x), der er uendeligt differentierbar på et interval. Antag f (x) er differentierbar på et interval centreret ved c. Så kraftserien, som er givet af

kaldes Taylor-serien udvidelsen af ​​funktionen f (

x

) omkring c. (Her f (n) (c) angiver n ^th derivatet ved x = ^c ). I Numerisk Analyse anvendes et begrænset antal udtryk i denne uendelige ekspansion til beregning af værdier på punkter, hvor serien er konvergeret til den oprindelige funktion. En funktion f (x) siges at være analytisk i intervallet (a, b), hvis for hver xε (a, b), Taylor-serien f (x) konvergerer til funktionen f (x). For eksempel er 1 / (1-x) analytisk på (-1, 1), da dens Taylor ekspansion 1 + x + x 2 + … + x n + … konvergerer til funktionen på dette interval, og ^e x ^{er analytisk overalt, da Taylorserien} e x ^{konvergerer til} e x < for hvert reelt tal ^x. Hvad er forskellen mellem Power Series og Taylor serien? ^{1. Taylor-serien er en speciel klasse af power-serier, der kun er defineret for funktioner, som uendeligt kan differentieres på et åbent interval.} 2. Taylor-serien tager specialformularen, mens en power-serie kan være en hvilken som helst serie af formularen